Heap

Arbori binari

Definiție

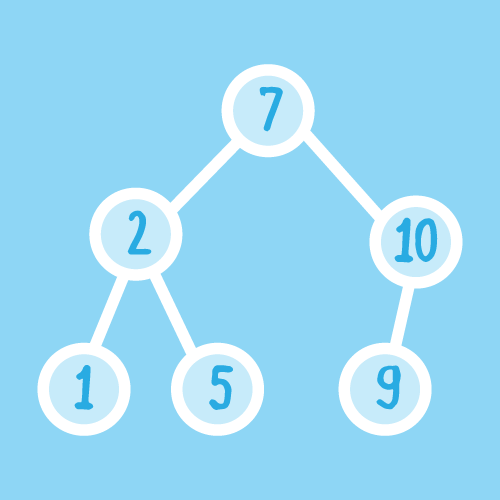 Un arbore binar este un arbore care fie este vid, fie constă dintr-un nod rădăcină si doi arbori binari disjuncți numiți subarborele stâng, respectiv subarborele drept.

Clase speciale:

 1) ARBORI BINARI STRICȚI sunt arborii binari în care orice vârf are gradul zero (este terminal) sau doi (are exact doi fii).
2) ARBORI BINARI PLINI sunt arbori binari care au 2^k-1 vârfuri dispuse pe nivelurile 0,1, ...,k-1, astfel încât pe fiecare nivel i se găsesc 2^i vârfuri.
3) ARBORI BINARI COMPLEȚI sunt arbori binari care se obțin dintr-un arbore binar plin prin eliminarea din dreapta către stanga a unor noduri de pe ultimul nivel.
G este conex minimal (dacă suprimăm o muchie, graful obținut este neconex)

Noțiuni Introductive

  1. Arbori
  2. Arbori binari
  3. Heap-uri

Generator Heap

Heap

  1. Creare
  2. Inserare nod
  3. Combinare
  4. Extragere nod

Coadă cu prioritate

Aplicații

Dicționar

Proprietați ale arborilor binari

 - Proprietatea 1 :: Numărul maxim de noduri de pe nivelul i al unui arbore binar este 2^i.
- Proprietatea 2 :: Numărul maxim de noduri într-un arbore binar cu înalțimea h este 2^(h+1)-1
- Proprietatea 3 :: În orice arbore binar nevid cu n noduri terminale există n-1 noduri de grad 2.
- Proprietatea 4 :: Un arbore cu n varfuri are înalțimea cel puțin egală cu [log n].
- Proprietatea 5 :: Definim lungimea drumurilor interne (I) ca fiind suma lungimilor drumurilor de la rădăcină la noduri neterminale (interne) si lungimea drumurilor externe (E) ca fiind suma lungimilor drumurilor de la rădăcină la noduri terminale (frunză sau externe). Într-un arbore binar cu n noduri interne, E=I+2*n.